컴퓨터가 정수를 표현하는 방법

정수를 표현하는 방법

정수를 표현하는 방법은 부호를 표시하지 않는 방법과 부호를 표시하는 방법으로 총 2가지 방법이 있다.

먼저 부호를 표시하지 않는 방법은 모든 비트를 양의 정수를 표현하는데 사용된다.

부호를 표시하는 경우는 양수와 음수를 구분해야 하기 때문에 다양한 방법으로 표현할 수 있다.

부호화 절대치

아래와 같은 3비트 2진수가 있다고 가정하자.

2진수	부호화 절대치
000	+0
001	+1
010	+2
011	+3
100	-0
101	-1
110	-2
111	-3

부호화 절대치는 최상위 비트로 양수와 음수를 구분하는 방식이다.

최상위 비트가 0이면 양수, 1이면 음수이다.

예를들어 111 이라는 수는 최상위 비트가 1이니 음수이고, 뒤로 이어지는 11을 10진수로 변환하면 3이다.

그렇기 때문에 -3 이라는 값을 가지게 된다.

부호화 절대치로 간단하게 음수를 표현했지만, 이상한 부분이 몇 가지 있다.

0이 왜 +0과 -0 두 개가 있을까?

그리고 2진수는 순차적으로 진행을 하는데, 10진수는 이상하게 값이 진행한다.

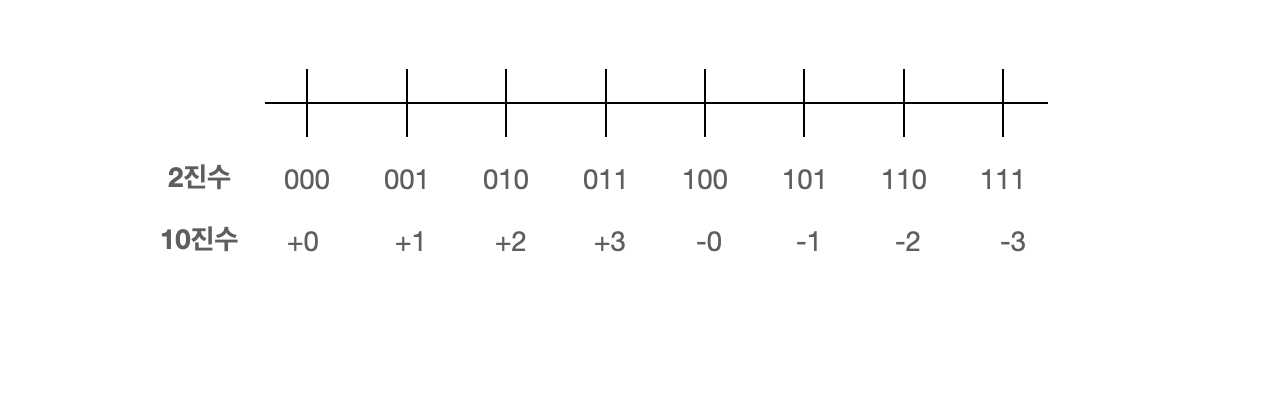
1의 보수

일반적인 수 체계와는 다르다는 것이 보인다.

이러한 점을 해결하기 위해 ‘보수’ 라는 방식을 사용하게 된다.

1의 보수는 +0과, -0을 아직 해결하지 못했지만, 수가 순차적으로 진행하도록 표현할 수 있다.

2진수	1의 보수
000	+0
001	+1
010	+2
011	+3
100	-3
101	-2
110	-1
111	-0

1의 보수를 사용하는 경우는 부호화 절대치와 마찬가지로 최상위 비트는 음,양수를 구분하는데 사용된다.

하지만 음수일 경우 모든 수를 반전시켜 값을 구하게 된다.

예를들어 111 이라는 수는 최상위 비트가 1이니 음수이고, 값을 반전시켜 000으로 변환한다.

이것을 10진수로 다시 변환하면 0이 되고, 음수이기 때문에 -0이 된다.

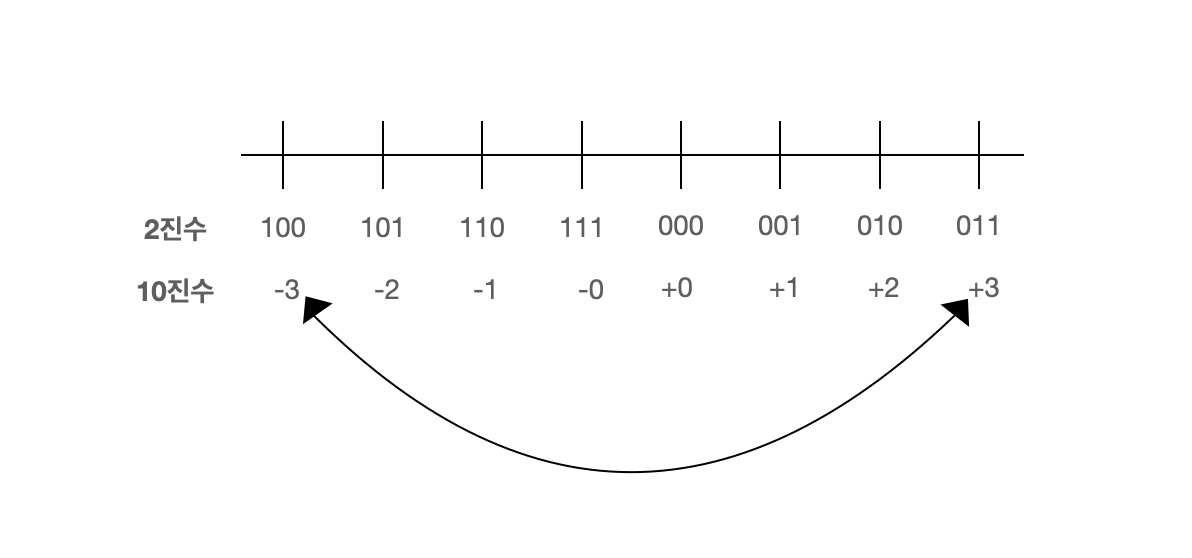
2진수 값의 위치를 이동 시켜 보면 1의 보수는 수가 순환하는 것을 볼 수 있다.

2의 보수

1의 보수를 사용함으로써 이제 수의 순환은 해결되었다.

아직 남은 문제는 +0과 -0인데 2의 보수를 사용하면 해결할 수 있다.

2진수	2의 보수
000	+0
001	+1
010	+2
011	+3
100	-4
101	-3
110	-2
111	-1

2의 보수를 구하는 방법은 다음과 같다.

먼저 2진수를 반전시켜 1의 보수로 변환을 시킨 후, +1을 해주면 2의 보수를 구할 수 있다.

예를들어 111 이라는 수는 최상위 비트가 1이니 음수이고, 값을 반전시켜 1의 보수인 000으로 변환한다.

여기서 1을 더해 001로 만든 후 10진수로 변환하면 1이되고, 음수이기 때문에 -1이 된다.

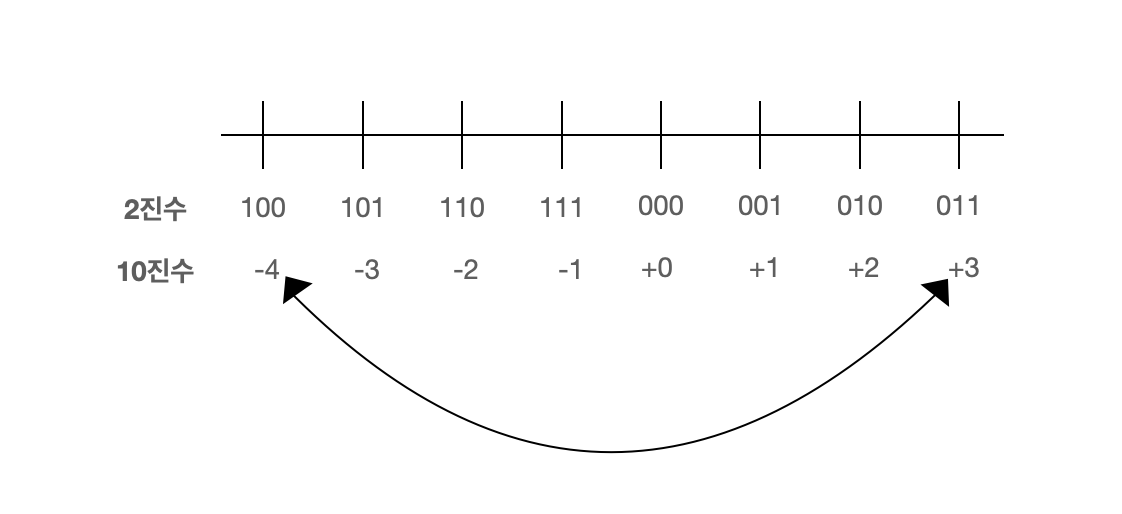
이제 0이 중복되지 않고, 일반적인 수 체계를 갖춘 것을 알 수 있다.

부동소수점

위에서 본 정수는 모두 고정소수점이다.

고정소수점은 말 그대로 소수점의 위치가 고정되어 있는 것을 의미하는데,

+32 라는 수는 사실 +32.0000… 이라는 값이고, 소수점 뒤는 모두 생략된다는 것이다.

부동소수점의 경우 1.2, -23.192 이런 값들을 의미한다.

이런 값들을 표현하기 위해 정규화 작업을 하게 된다.

부동소수점	표현
1.2	0.12 x 101
-23.192	-0.23192 x 102
0.00023	0.23 x 10-3

소수점 아래 수는 가수, 10의 제곱수는 지수, 그리고 +와 -는 부호로 분리하여 표기한다.

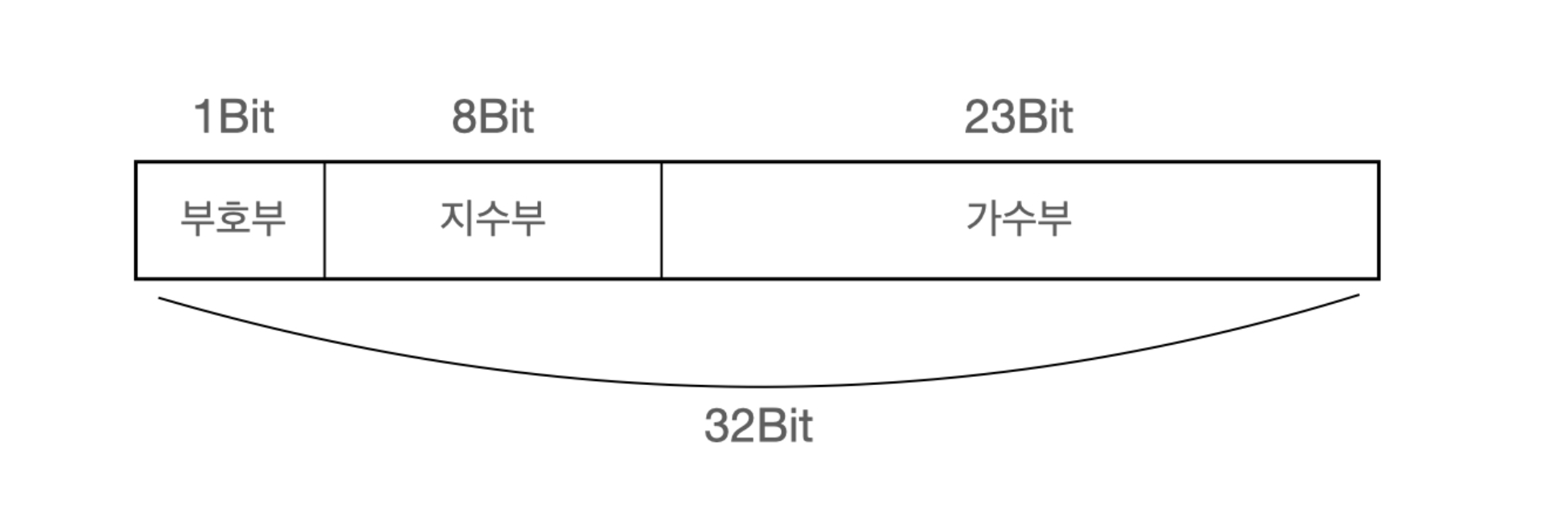
이러한 포맷을 IEEE 754 포맷이라고 한다.

56.125 라는 값을 IEEE 754 포맷에 맞춰 표기해보자.

먼저 56.125는 양수이기 때문에 부호부는 0이다.

그리고 56.125를 2진수로 변환하여 111000.001 값을 만든다.

소수점을 첫번째 자리는 유효 자리로 놔두고 1.11000001 x 2⁵ 로 변환한다.

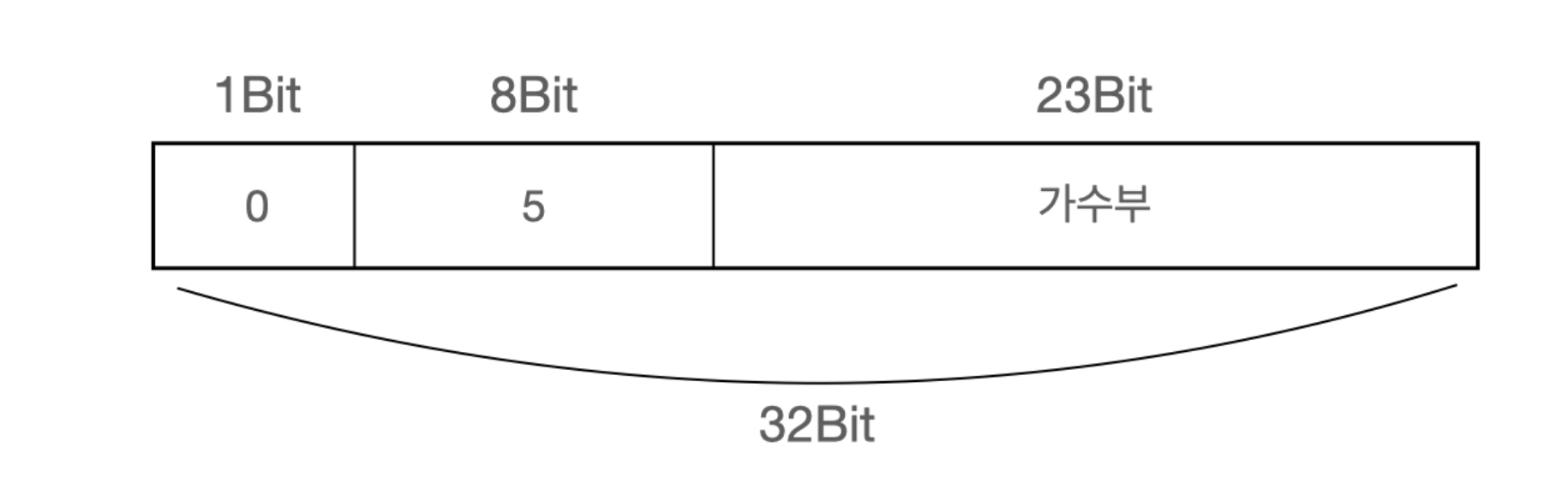
그런데 지수부는 8비트로 256개의 수를 표현한다.

지수부 역시 음수가 표현될 수 있기 때문에 5를 바로 2진수로 변환하지 않고,

256의 절반을 잘라 127을 기준으로, 127보다 작으면 음수, 127보다 크면 양수로 표현한다.

즉 지수부 5를 표현하기 위해선 127 + 5인 132 즉 2진수 10000100를 저장해야한다.

가수부는 소수점 아래 수를 표기하되 앞에서부터 작성해야하고, 모자른 부분은 모두 0을 붙여 표현한다.

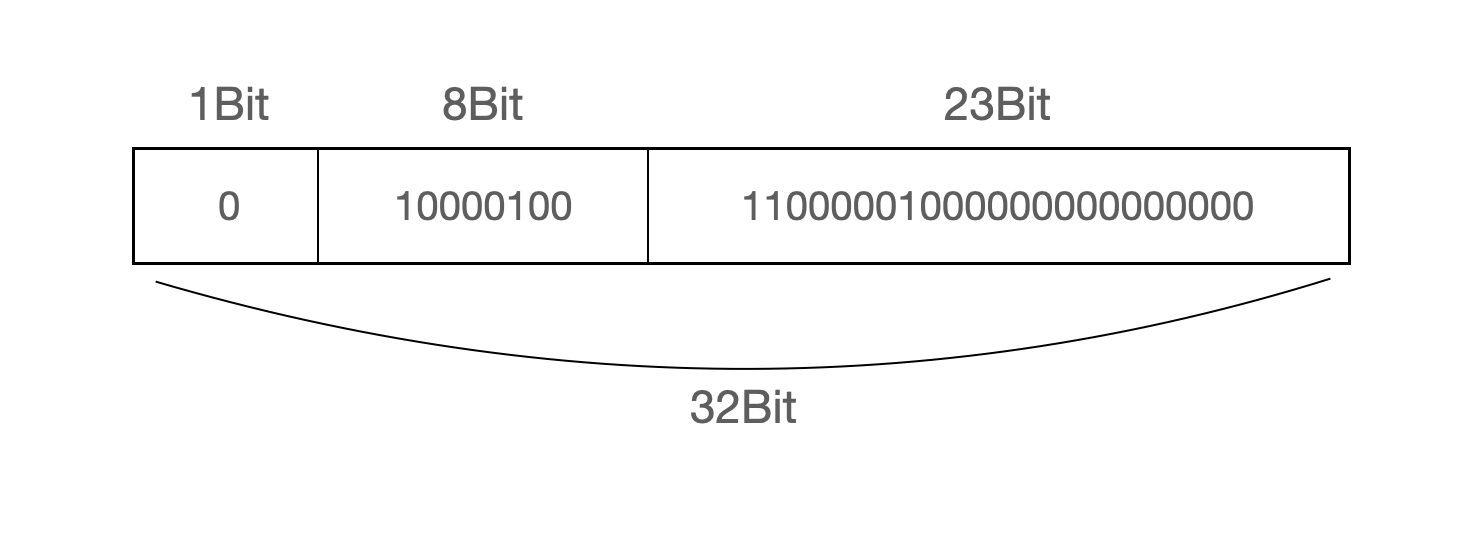
최종적으로 부동소수점을 IEEE 754 포맷에 맞춰 작성하면 아래와 같은 형태가 된다.